求一个数的平方根
求解平方根主要有两种方法，一种是利用二分法，另外一种是牛顿迭代法，后一种迭代的速度很快。
牛顿迭代法
牛顿迭代公式为：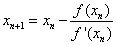
求解 f(x) = x^2 - A = 0 的公式为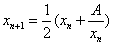
对牛顿迭代法的理解可以参考这篇文章
对于求平方根公式还可以这样理解理解，想象把一个长方形压缩成一个面积相同的正方形的过程，此时 x 为长方形一条边的长度，而 A/x 为邻边的长度，每次迭代取这两条边的平均数，于是这个长方形会越来越像正方形。
二分法
可以有两种思考方式，一种是 f(x) = x^2 - A， 由于在 x 为正数范围内函数是单调递增的，若中间点的函数值小于0，则将左端点右移，大于 0 则将右端点左移。
也可以这样考虑，将问题转化为求满足条件C: f(x) <= A 的最大的 x，搜索区间的下界是0，上界是A，初始下界满足条件，上界是不满足条件。若中间点满足条件C, 显然中间点符合要求，但是我们还想看看有没有更好的结果，于是我们将下界加大为 mid，若不满足条件则将上界缩小，循环100次后或合适精度后中止，最终的答案是下界。