发表于

描述
累加一棵树的左叶子结点的值。

输入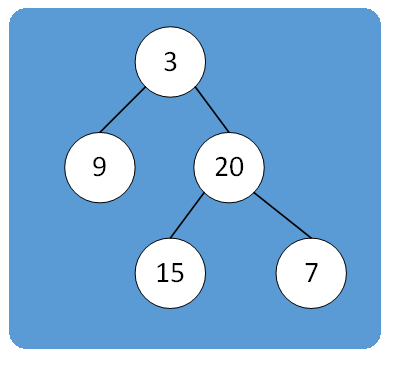





输出
24 (9+15)

解决思路
root->left && !(root->left->right) && !(root->left->left)用来判断是否是左叶子结点。递归函数返回的为
f(该节点左孩子)+ f(该节点右孩子)的形式。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    int sumOfLeftLeaves(TreeNode* root) {
        int res = 0;
        if (root == NULL) { return 0; }
        //left leave.
        if (root->left && !(root->left->left) && !(root->left->right)) {
            res = root->left->val;
        }
        res += sumOfLeftLeaves(root->left) + sumOfLeftLeaves(root->right);
        return res;
    }
};

参考资料
原题链接

发表于

二维数组

考虑将一个二维数组表示成一维的形式，比如 a[3][4] 最后的一个下标为 a[11]
i * 4 + j 就是计算下标的，以最后一个数字的下标11为例，row = 11/4 col = 11%4

发表于

Subsequence POJ No.3061

给定长度为 n 的数列整数 a[0], a[1], a[2],…,a[n-1],以及整数 S。求出总和不小于 S 的连续子序列的最小值。

样例

1
2
输入: n = 10,S = 15,a = {5,1,3,5,10,7,4,2,8};
输出: 2 (5+10)

思路
思路1：累加得到序列b[n],其中b[i] = a[0]+a[1]+…+a[i],i>=0,再利用二分搜索从 i 到 n-1 查找第一个大于 S 的值。
思路2：像虫子一样向前挪动。

notes: lower_bound(b+i,b+n, S + b[i]) 返回的是地址，减去 b 的首地址，即得到下标

1
2
3
4
5
6
7
8
9
10
11
12
13
int solve(int a[], int n,int S) {
    int b[100] = {0};
    for (int i = 0; i < n; i++) {
        b[i + 1] = a[i] + b[i];
    }
    if (b[n] < S) { return -1; }
    int res = n;
    for (int i = 0; b[n] - b[i] >= S; i++) {
        int t = lower_bound(b+i,b+n, S + b[i]) - b;
        res = min(res, t-i);
    }
    return res;
}

尺取法

1
2
3
4
5
6
7
8
9
10
11
12
13
int solve3(int a[], int n, int S) {
    int s = 0, t = 0, sum = 0, res = n + 1;
    for (;;) {
        while (sum < S && t < n) {
            sum += a[t++];
        }
        if (sum < S) { break; }
        res = res < t - s  ? res : t - s ;
        sum -= a[s++];
    }
    if (res <= n) { return res; }
    return -1;
}

发表于

prim 算法

思路
每次选取一个结点，记已选择的点的集合为 X ,计算未选择的点与 X 集合中结点的权值，选择一个权值最小的结点加入到 X 中。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
int prim() {
    int v = 0;
    int sum = 0;
    int visited[N] = {false};
    visited[0] = true;
    for (int i = 0; i < N-1; i++){
        int minval = INF;
        int t1 = v;
        int t2 = v;
        for (int j = 0; j < N; j++) {
            if (visited[j]) { continue; }
            //下面这个循环是判断已有的点集合和当前点的最小距离
            for (int k = 0; k < N; k++) {
                if (visited[k]) {
                    if (d[k][j] < minval) {
                        t1 = k; t2 = j;
                        minval = d[k][j];
                    }
                }
            }
        }
        sum += minval;
        visited[t2] = true;
    }
    return sum;
}

代码2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
int prim_demo() {
    int used[N] ;
    int mincost[N] ;
    for (int i = 0; i < N; i++) {
        used[i] = false;
        mincost[i] = INF;
    }
    int res = 0;
    mincost[0] = 0;
    while (true) {
        int v = -1;
        for (int u = 0; u < N; u++) {
            if (!used[u] && (v == -1 || mincost[u] < mincost[v])) { v = u; }
        }
        if (v == -1) { break; }
        used[v] = true;
        res += mincost[v];

        for (int u = 0; u < N; u++) {
            mincost[u] = min(mincost[u], d[v][u]);
        }
    }
    return res;
}

Kruskal 算法

思路
每次选取权值最小的边，若加入后不构成环，则将这条边加入

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
int u[maxn],v[maxn],w[maxn],r[maxn],p[maxn];
int n,m;

int cmp(const int i,const int j){
    return w[i]<w[j];
}

// 并查集 find
int findp(int x){return x==p[x]?x:p[x] = findp(p[x]);}

int Kruskal(){
    // init index and union-find
    for(int i=0;i<m;i++) p[i] = r[i] = i;

    sort(r,r+m,cmp);

    int sum =0;
    for(int i=0;i<m;i++){
        int e = r[i];int x = findp(u[e]);int y = findp(v[e]);
        if(x!=y){//不连通
            sum += w[e]; p[x] = y;
        }
    }
    return sum;
}