【挑战程序设计竞赛】 TSP 状态压缩动态规划

发表于 2018-09-26

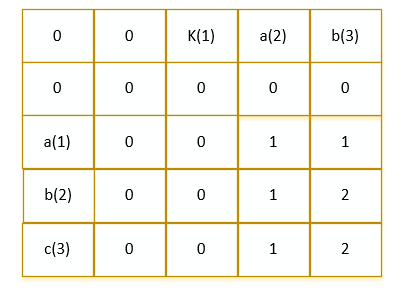
描述
其中 S 为未访问的城市集合，v为当前所在城市，d[v][u]为由 v 城市到 u 城市之间的距离。利用二进制01来保存访问的状态。第一个返回条件很好理解，就是记忆搜索。对于第二个和第三个需要好好理解一下。 dp[11111][4] 的值为无穷大，它不会经过循环，而是直接赋值。不用担心第一次的分支 dp[00001][0]没有出口，这个值肯定不是最小的，很可能是无穷大。

notes: 1<<n 代表1左移 n 位

int rec(int S, int v) {
    if (dp[S][v] >= 0) {
        return dp[S][v];
    }
    if (S == (1 << n) - 1 && v == 0) {
        return 0;
    }
    int res = BIGNUM;
    for (int u = 0; u < n; u++) {
        if (!(S >> u & 1)) {
            res = min(res, rec(S | 1 << u, u) + d[v][u]);
        }
    }
    return dp[S][v] = res;
}

1 2	//利用这一条语句进行调用，即最终结果 rec(0, 0)

【挑战程序设计竞赛】二分法

发表于 2018-09-26

描述
n条绳子，第i条绳子长度为a[i],切割成长度相同的k段，求能切割出最大的长度

样例

1 2	输入: n = 4; k =11 a = {8.02,7.43,4.57,5.39}; 输出: 2.00 (每条绳子分割可以得到4条，3条，2条，2条，共11条绳子)

思路
将这题转化为求满足 C(x) 的最大的 x,解范围下界是个较小的可行解，上界是一个较大的不可行解，每次取中间值缩小解范围。

代码

bool C(vector<double> a,int K,double x) {
    int len = a.size();
    int sum = 0;
    for (int i = 0; i < len; i++) {
        sum += int(a[i] / x);
    }
    return sum >= K;
}

void solve(vector<double> a, int K) {
    double lo = 0;                //下界，显然0是可行解，但很不优，需要向上扩充
    double hi = 10000;            //上界，不可行解，需要向下收缩
    //循环100次是为了尽量缩小解的范围
    for (int i = 0; i < 100; i++) {
        double mid = lo + (hi - lo) / 2;
        if (C(a, K, mid)) { lo = mid; }
        else { hi = mid; }
    }
    printf("%.2lf", lo);
}

c/c++ 随机数

发表于 2018-09-26

c风格的随机数

#include<stido.h>
#include<time.h>

int main(){
    srand(time(0));
    rand();  //rand()为0到最大的int值
}

c++ 标准库

#include<random>
#include<ctime>

default_random_engine e(time(0));
std::uniform_real_distribution<double> u(0, 1);//包括 0 ，不包括 1
std::uniform_int_distribution<int> dis1(0, 100);//包括 0 和 100

double p = u(e); //p在0到1之间

uniform_int_distribution的随机数的范围不是半开范围[ )，而是[ ]，对于uniform_real_distribution却是半开范围[ )。

2018年9月25日

发表于 2018-09-25

java写入文件

PrintWriter writer = new PrintWriter("the-file-name.txt", "UTF-8");
writer.println("The first line");
writer.println("The second line");
writer.close();

如果要写入数值类型，可以进行转换

1	String s = String.valueOf(123);

2018年9月23日

发表于 2018-09-23

android开发

在布局文件中，点击 preview 无法显示部件。
解决方法: 将 res/values/style.xml 中的

1	<style name="AppTheme" parent="Theme.AppCompat.Light.DarkActionBar">`

修改为:

1	<style name="AppTheme" parent="Base.Theme.AppCompat.Light.DarkActionBar">

参考文章1,参考文章2

【挑战程序设计竞赛】最长公共子序列

发表于 2018-09-22

描述
给定字符串S和T，求最长公共子串的长度
假设S = "kabc",T = "abcd" 则长度应该为3

思路
比较两个字符串的每一个字符，可能会产生以下情况：

S[i+1] = T[j+1] –> dp[i+1][j+1] = dp[i][j]+1
S[i+1] = T[j] –> dp[i+1][j+1] = dp[i+1][j]
S[i] = T[j+1] –> dp[i+1][j+1] = dp[i][j+1]
第二种情况和第三种情况均没有产生新的值，只是传递而已。

代码

int maxCommonString(const string & S, const string & T) {
    int lenS = S.size();
    int lenT = T.size();
    vector<vector<int> >dp(lenS + 1, vector<int>(lenT + 1, 0));
    for (int i = 0; i < lenS; i++) {
        for (int j = 0; j < lenT; j++) {
            if (S[i] == T[j]) {
                dp[i + 1][j + 1] = dp[i][j] + 1;
            }
            else {
                dp[i + 1][j + 1] = max(dp[i + 1][j], dp[i][j + 1]);
            }
        }
    }
    return dp[lenS][lenT];
}

【挑战程序设计竞赛】背包问题

发表于 2018-09-21

描述
n个物品，有不同的重量weight[n],有不同的价值price[n]
你有一个能承载重量为A的背包，问能带走的最大价值是多少。

暴力搜索
每一个物品都有可能带走或者不带走，枚举出所有情况，此时可以采用深度优先搜索。

notes:price+0代表最后一个节点的价值，dfs+price中price表示保存当前价值，再看看加上后续的点会不会更优解，可以用二叉树理解。

int dfs(int i,int j) {
    if (i == n) {
        return 0;
    }
    if (j < weight[i]) {
        //can not take the item
        return dfs(i+1,j);
    }
    else {
        //can take the item or not take it
        return max(dfs(i+1,j), dfs(i + 1, j - weight[i]) + price[i]);
    }
}

记忆搜索1

int dp1[100][100];

int dfs2(int i, int j) {
    int res = 0;
    if (dp1[i][j] != 0) {
        return dp1[i][j];
    }

    if (i == n) {
        res =  0;
    }
    else if (j < weight[i]) {
        //can not take the item
        res =  dfs2(i + 1, j);
    }
    else {
        //can take the item or not take it
        res =  max(dfs2(i + 1, j), dfs2(i + 1, j - weight[i]) + price[i]);
    }
    return dp1[i][j] = res;
}

记忆搜索2

int solve() {
    vector<vector<int>> dp2(n+1,vector<int>(A+1,0));
    for (int i = n-1; i >= 0; i--) {
        for (int j = 0; j <= A; j++) {
            if (j < weight[i]) {
                dp2[i][j] = dp2[i + 1][j];
            }
            else {
                dp2[i][j] = max(dp2[i + 1][j], dp2[i + 1][j - weight[i]] + price[i]);
            }
        }
    }
    return dp2[0][A];
}

递推法
dp[i+1][j]为前i个物品负重为j的最大价值。
当i=0时，为dp[0+1][j]代表的含义为一个物品重量为j的最大价值。
dp[2][10] = max{dp[1][10],dp[1][10-weight[1]]+price[1]};
物品和价值都是从0开始的，也就是说weight[1]实际上代表的就是第二个的重量。

int solve2() {
    vector<vector<int>>dp3(n + 1, vector<int>(A + 1, 0));
    for (int i = 0; i < n; i++) {
        for (int j = 0; j <= A; j++) {
            if (j < weight[i]) {
                dp3[i + 1][j] = dp3[i][j];
            }
            else {
                dp3[i + 1][j] = max(dp3[i][j], dp3[i][j - weight[i]] + price[i]);
            }
        }
    }
    return dp3[n][A];
}

转移状态
一个物品的选用和不选用两种状态，也就是会影响前i+1个物品最大负重量为j(不选中)和j-weight[i+1](选中)。

int solve3() {
    vector<vector<int>> dp4(n + 1, vector<int>(A + 1, 0));
    for (int i = 0; i < n; i++) {
        for (int j = 0; j <= A; j++) {
            dp4[i + 1][j] = max(dp4[i + 1][j], dp4[i][j]);
            if (j + weight[i] <= A) {
                dp4[i + 1][j + weight[i]] = max(dp4[i + 1][j + weight[i]], dp4[i][j] + price[i]);
            }
        }
    }
    return dp4[n][A];
}

【leetcode】 406 Queue Reconstruction by Height

发表于 2018-09-20

描述
给定一些数字，要求重新排序

input:
[[7,0], [4,4], [7,1], [5,0], [6,1], [5,2]]

Output:
[[5,0], [7,0], [5,2], [6,1], [4,4], [7,1]]

每一组数据有两个数字组成，要求每组数据第二个数据为排在它前面大于等于它的数字的个数。
比如[5,2]在它前面有两个数据都大于等于它。

初始数据[[7,0], [4,4], [7,1], [5,0], [6,1], [5,2]]

思路

找出最大的数，再对它根据第二个数排序，得到[[7,0],[7,1]]
找出第二大的数，同样的排序，得到[6,1]
将[6,1]插入，得到[[7,0],[6,1],[7,1]]
找出第三大数，[[5,0],[5,1]]插入得到[[5,0],[5,1],[7,0],[6,1],[7,1]]
找出第四大数，[4,4],插入得到[[5,0],[5,1],[7,0],[6,1],[4,1],[7,1]]
DONE。

vector没有自带的find(),set和map有
map<int,vector<int>>后面的不会自动排序，而改成map<int,set<int>>可以排序
markdowm中的<和>需要转义，利用⁢和>
map插入数据mymap.insert({1,1}),加入大括号，或者mymap.insert(std::pair<int,int>(1,1))

我的代码

class Solution {
public:
    vector<pair<int, int>> reconstructQueue(vector<pair<int, int>>& people) {
        map <int, set<int>> peo;
        for (int i = 0; i < people.size(); i++) {
            auto p = people[i];
            peo[p.first].insert(p.second);
        }
        vector<pair<int, int>> result;
        for (auto iter = peo.rbegin(); iter!= peo.rend(); iter++) {
            for (auto iter2 = iter->second.begin(); iter2 != iter->second.end(); iter2++) {
                result.insert(result.begin() + *iter2, { iter->first,{*iter2} });
            }
        }
        return result;
    }
};

值得学习的代码
原文链接

class Solution {
public:
    vector<pair<int, int>> reconstructQueue(vector<pair<int, int>>& people) {
        auto comp = [](const pair<int, int>& p1, const pair<int, int>& p2)
        { return p1.first == p2.first ? p1.second < p2.second : p1.first > p2.first; };
        sort(people.begin(), people.end(), comp);
        vector<pair<int, int>> res;
        for (auto& p : people) {
            res.insert(res.begin() + p.second, p);
        }
        return res;
    }
};

参考资料
原题链接

【挑战程序设计竞赛】二分搜索

发表于 2018-09-19

最近看了许多的算法内容都和这个东西有关，从最开始的编程题求峰值，到中间选取任意个数等于一个固定值问题，将二分法与链表结合，有了二叉查找树，红黑数等等。

来看一个题目：从一个装有n张卡片的口袋里面有放回的选取4张卡片，给定一个值m，判断存在这4张卡片的总和为m。
样例输入1:

1
2
3

3
1 ,2 ,3
4

这种情况答案应该是存在和为4的，比如1，1，1，1。

样例输入2:

1
2
3

3
4 ,2 ,3
4

显然这种情况不存在总和为4的情况。

解决这个问题最简单的方法就是暴力枚举，O(N^4)。
暴力枚举

bool selok(vector<int> nums, int m) {
    int len = nums.size();
    for (int i = 0; i < len; i++) {
        for (int j = 0; j < len; j++) {
            for (int k = 0; k < len; k++) {
                for (int ind = 0; ind < len; ind++) {
                    if (nums[i] + nums[j] + nums[k] + nums[ind] == m) {
                        return true;
                    }
                }
            }
        }
    }
    return false;
}

二分搜索1个变量
时间复杂度O(N^3*log2(N))

bool selok2(vector<int> nums, int m) {
    int len = nums.size();
    sort(nums.begin(), nums.end());
    for (int i = 0; i < len; i++) {
        for (int j = 0; j < len; j++) {
            for (int k = 0; k < len; k++) {
                if (binsearch(nums, m - nums[i] - nums[j] - nums[k])) { return true; }
            }
        }
    }
    return false;
}

二分搜索两个变量
时间复杂度O(N^2*log2(N))

bool selok3(vector<int> nums, int m) {
    int len = nums.size();
    vector<int> nums_sum;
    for (int i = 0; i < len; i++) {
        for (int j = 0; j < len; j++) {
            nums_sum.push_back(nums[i] + nums[j]);
        }
    }
    sort(nums_sum.begin(), nums_sum.end());
    for (int i = 0; i < len; i++) {
        for (int j = 0; j < len; j++) {
            if (binsearch(nums_sum, m - nums[i] - nums[j])) { return true; }
        }
    }
    return false;
}

二分法

bool binsearch(vector<int>&nums, int target) {
    int left = 0;
    int right = nums.size() - 1;
    while (left <= right) {
        int mid = (left + right) / 2;
        if (nums[mid] == target) { return true; }
        else if (nums[mid] < target) { left = mid + 1; }
        else { right = mid - 1; }
    }
    return false;
}

notes:二分法边界控制有点麻烦，要小心。比如(left+right)/2没有left+(right-left)/2好，前者可能会溢出。参考文章

【编程之美】1.15 构造数独

发表于 2018-09-18

深度优先搜索
dfs(0,0)开始直到d(8,8),就完成了，可以参考:

notes:int maxrow = (irow/3)+3得到的是每一个宫里面的行数目最大值。

直接构造
这种方法有较大的局限性，生成的数独有规律，但是很快。
大致思路是，在中间的宫5里面随机生成数字，之后调行换位置形成左边宫4的位置，以及右边6的位置。持续将上2,下8一并完成了。
之后利用4补全1和7，利用6补全3和9，简单粗暴。

notes:<img src="2018-9-18-blog/sudu.png" width="50%" height="50%" />可以实现调整图片大小。